Talking about global warming

Two degrees Celsius, that’s it?

This week The Economist reported on our trajectory toward the global average temperature threshold set by the 2015 Paris Agreement, no more than 2°C (3.6°F) above pre-industrial levels. It struck me how little intuition I have about the consequences of that increase — it still sounds so benign no matter how many articles I read telling me otherwise.

Taking notes from communicating flood risk

This reminded me of an old 538 article about how the concept of a “100-year floodplain” — first introduced by the US government in 1973 — is not at all self-explanatory, and at best misleading. Instead, a more direct way to frame the same concept is that there is a one-in-four chance of a flood within 30 years (i.e. a typical mortgage duration), a fact that can be derived through basic probability theory.

Two degrees on average -> four times the extreme heat!

How can we reframe a 2°C shift in average temperatures into something more meaningful? By reminding ourselves that a small shift in the mean of a distribution can lead to significant increases in the frequency of extreme observations. And that’s more meaningful because while none of us directly experience the mean annual temperature, we do experience individual very hot days!

The following is a gross simplification and not climate science, but it illustrates how a 2°C shift in mean temperature is consistent with a 3-5x increase in the frequency of very hot days.

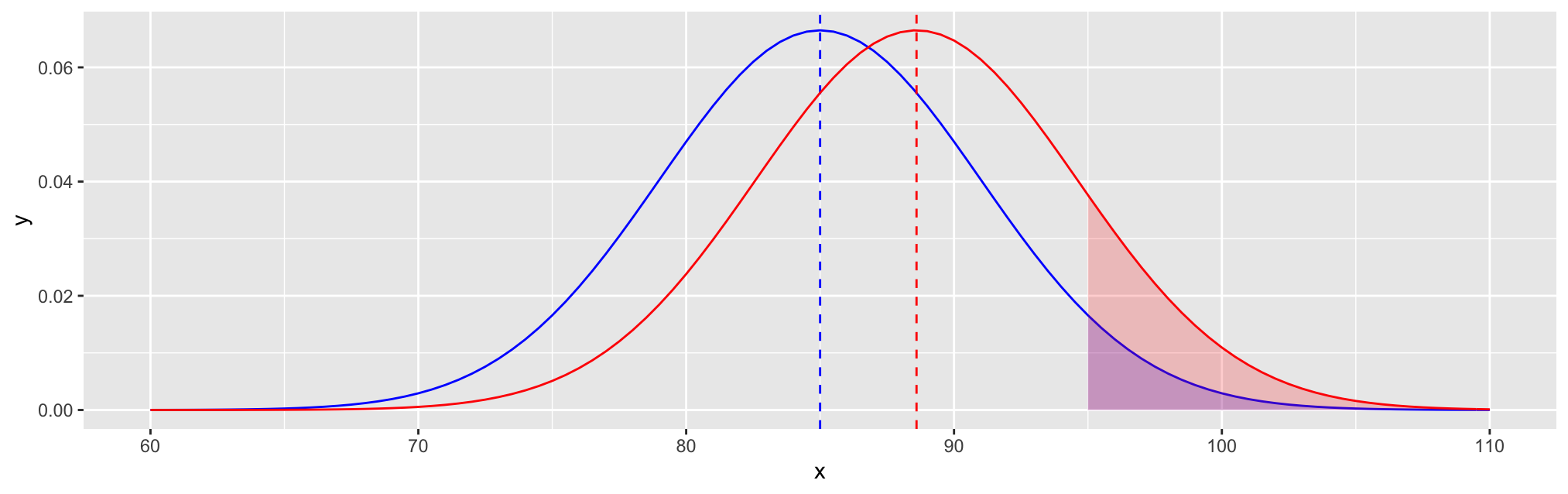
The blue curve plots the probability density of the July 25 daily high temperature in Central Park, based on historical data, which has mean m0 = 85 and standard deviation sd = 6. The mean of red curve has been shifted by 3.6°F (2°C), m1 = 88.6. The effect of this is that the probability of a hot 95°F day (the shaded area beneath the curve), nearly triples h1/h0 = 2.99, and the probability of an extremely hot 100°F day increases over four-fold, vh1/vh0 = 4.62.

library(tidyverse)

m0 <- 85
m1 <- 85 + 2 * (9/5)
sd <- 6

x_hot <- 95
x_vhot <- 100

ggplot(data.frame(x = c(60, 110)), aes(x = x)) +
  geom_vline(xintercept = m0,
             linetype = "dashed",
             color = "blue") +
  stat_function(fun = dnorm,
                geom = "line",
                color = "blue",
                args = list(m0, sd)) +
  stat_function(fun = dnorm, 
                geom = "area",
                xlim = c(x_hot, 110),
                alpha = .2,
                fill = "blue",
                args = list(m0, sd)) +
  geom_vline(xintercept = m1,
             linetype = "dashed",
             color = "red") +
  stat_function(fun = dnorm,
                geom = "line",
                color = "red",
                args = list(m1, sd)) +
  stat_function(fun = dnorm, 
                geom = "area",
                xlim = c(x_hot, 110),
                alpha = .2,
                fill = "red",
                args = list(m1, sd))

h0 <- pnorm(x_hot, mean = m0, sd = sd, lower.tail = FALSE)
h1 <- pnorm(x_hot, mean = m1, sd = sd, lower.tail = FALSE)
h1/h0

vh0 <- pnorm(x_vhot, mean = m0, sd = sd, lower.tail = FALSE)
vh1 <- pnorm(x_vhot, mean = m1, sd = sd, lower.tail = FALSE)
vh1/vh0